目次
必要なライブラリ
- matplotlib
- numpy
以上の二つが今回必要となるライブラリになります。この二つがまだインストールされていない方は、windowsの場合はコマンドプロンプトから下記のように入力してパッケージをインストールしてください。
$ pip install matplotlib
$ pip install numpyこの二つのライブラリは今後も頻繁に使用するライブラリなので、早いうちから慣れていきましょう。
pythonでアニメーションを表現するには
pythonでアニメーションをプログラムするには、matplotlib.animationを使用します。下のmatplotlibの公式リンクから使い方を確認することができます。
https://matplotlib.org/api/animation_api.html?highlight=animation#module-matplotlib.animation
今回は時間変化する位置xにおける電圧、電流値を2次元で表現したいので、事前にx、y座標の時間変化のグラフを作成して、アニメーションにする方法で表現していきたいと思います。
そこで、matplotlib.animation.ArtistAnimationというメソッドを使います。
定在波の導出
今回は、伝送線路における定在波を表現していきたいと思います。下の図のような一般的な伝送線路を想定します。線路の特性インピーダンスは(損失なしの場合)、変数がxだけのとき、
$$V(x)=Ae^{-jβx}+Be^{jβx}$$
$$I(x)=(Ae^{-jβx}-Be^{jβx})/Z_0$$
$$Z_0:線路の特性インピーダンス$$
と表すことができ、時間領域に拡張すると、
$$V(x,t)=V(x)e^{jωt}, I(x,t)=I(x)e^{jωt}$$
と波動方程式より求めることができる。ここから、電圧、電流の瞬時値を求めるためには複素数の実数成分を求めるので、
電圧の瞬時値は、
$$v(x,t)=Acos(ωt-βx)+Bcos(ωt+βx)$$
電流の瞬時値は、
$$i(x,t)={Acos(ωt-βx)+Bcos(ωt+βx)}/Z_0$$
となり、それぞれの第一項は+x方向に進む波、第二項は-x方向に進む波を表している。

今回は電圧の瞬時値の可視化を行うので、電圧の式を変形していく。
AとBの関係は反射係数Sで決まる。Z_Lを終端負荷とすると、
$$S=(反射波の大きさ)/(入力波の大きさ)$$
$$S=B/A=(Z_L-Z_0)/(Z_L+Z_0)$$
となり、終端負荷にAとBは依存する。
- 開放終端・・・Z_L=0[Ω]
- 短絡終端・・・Z_L=∞[Ω]
- 整合終端・・・Z_L=Z_0[Ω]
上の式より、整合終端の場合は反射波が線路に理論上存在しないことになる。つまり、電力伝送効率100%である。しかし、実際は線路の損失があり、少なからずは電力効率が下がっている。
整合終端の式
電圧の反射係数は0となり、B=0となる。このとき、瞬時値は、
$$v(x,t)=Acos(ωt-βx)$$
開放終端の式
電圧の反射係数はS=1となり、B=Aとなる。このとき、瞬時値は、
$$v(x,t)=Acos(ωt-βx)+Acos(ωt+βx)$$
短絡終端の式
電圧の反射係数はS=-1となり、B=-Aとなる。このとき、瞬時値は、
$$v(x,t)=Acos(ωt-βx)-Acos(ωt+βx)$$
プログラムの実装
実際に開放終端の場合の電圧の瞬時値を表すためのpythonコードが以下のようになります。
以下の条件でシミュレーションしました。
- 電源周波数:3GHz
- 電圧の伝わる速さ:光速
- A=1、B=1
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
#環境設定
c = 3e8 #光速 m/s
f = 3e9 #周波数 Hz
T = 1 / f #周期 s
ramda = c / f #波長 m
beta = 2 * np.pi / ramda #位相定数
omega = 2 * np.pi / T #角周波数
x_range = np.linspace(-4*np.pi/beta, 0.0, 200)
t_range = np.linspace(0.0, 2*np.pi/omega, 100)
#x, y 座標上で時間tを変化させる
fig = plt.figure()
artists = []
for t in t_range:
v = np.cos(omega*t - beta*x_range) + np.cos(omega*t + beta*x_range)
im = plt.plot(x_range,v, color = "blue")
artists.append(im)
ani = animation.ArtistAnimation(fig, artists,50)
ani.save('animation_test.gif')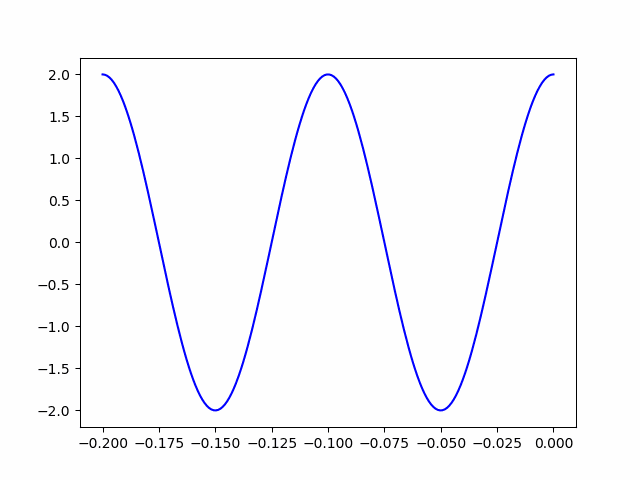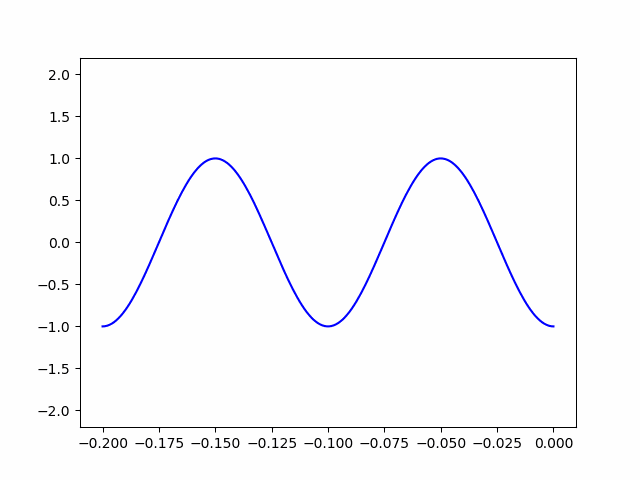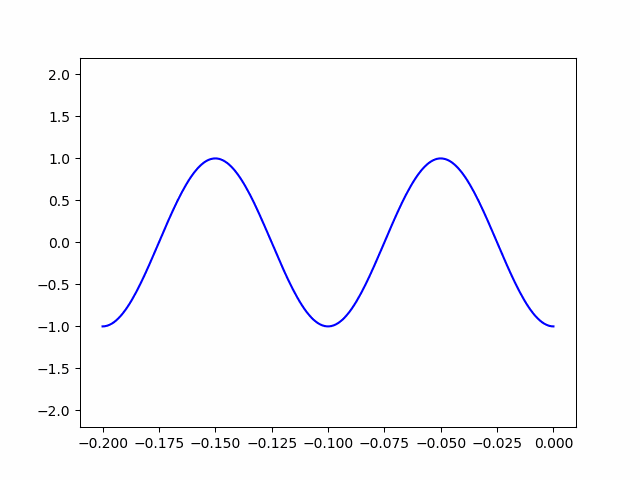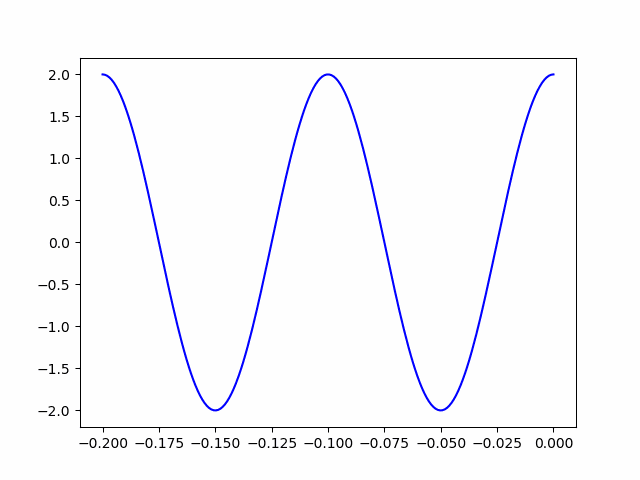
上の動画がコード(ani.save(‘animation_test.gif’))で保存されたものです。波長が10cmで、終端で最大値を取っているので、望通りの結果を得ることができました。コードのvの値を少しいじるだけで短絡終端や整合終端の定在波の記述ができるので、ぜひやってみて下さい。








コメントを残す